Human Pose, Shape and Action
3D Pose from Images
2D Pose from Images
Beyond Motion Capture
Action and Behavior
Body Perception
Body Applications
Pose and Motion Priors
Clothing Models (2011-2015)
Reflectance Filtering
Learning on Manifolds
Markerless Animal Motion Capture
Multi-Camera Capture
2D Pose from Optical Flow
Body Perception
Neural Prosthetics and Decoding
Part-based Body Models
Intrinsic Depth
Lie Bodies
Layers, Time and Segmentation
Understanding Action Recognition (JHMDB)
Intrinsic Video
Intrinsic Images
Action Recognition with Tracking
Neural Control of Grasping
Flowing Puppets
Faces
Deformable Structures
Model-based Anthropometry
Modeling 3D Human Breathing
Optical flow in the LGN
FlowCap
Smooth Loops from Unconstrained Video
PCA Flow
Efficient and Scalable Inference
Motion Blur in Layers
Facade Segmentation
Smooth Metric Learning
Robust PCA
3D Recognition
Object Detection
Robust PCA
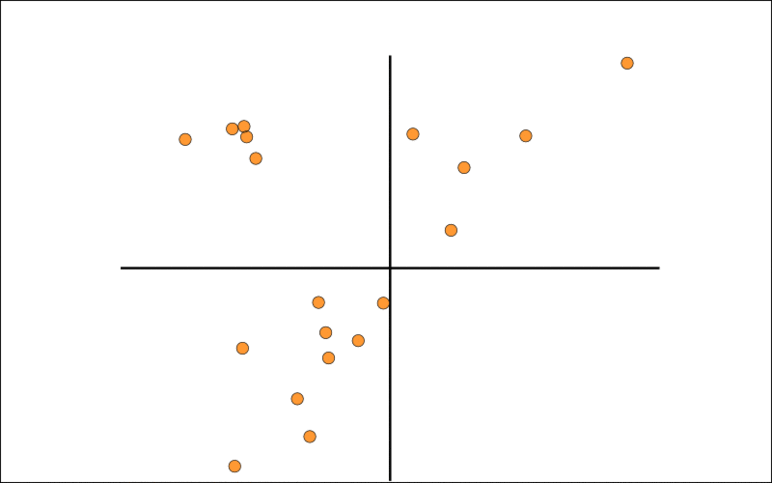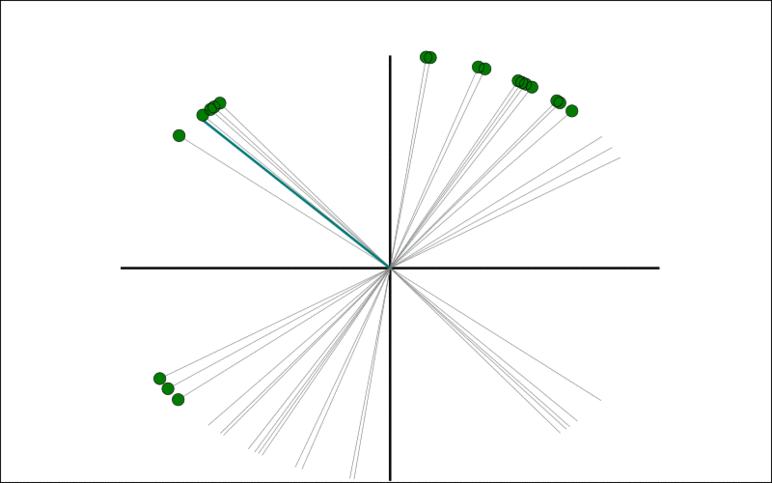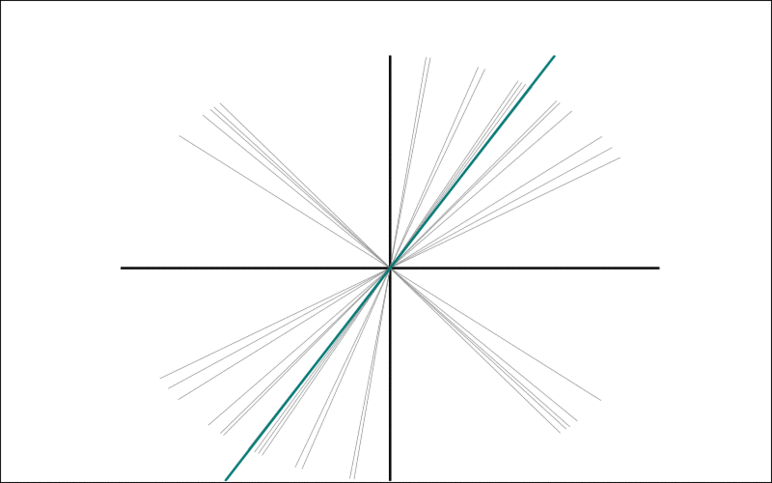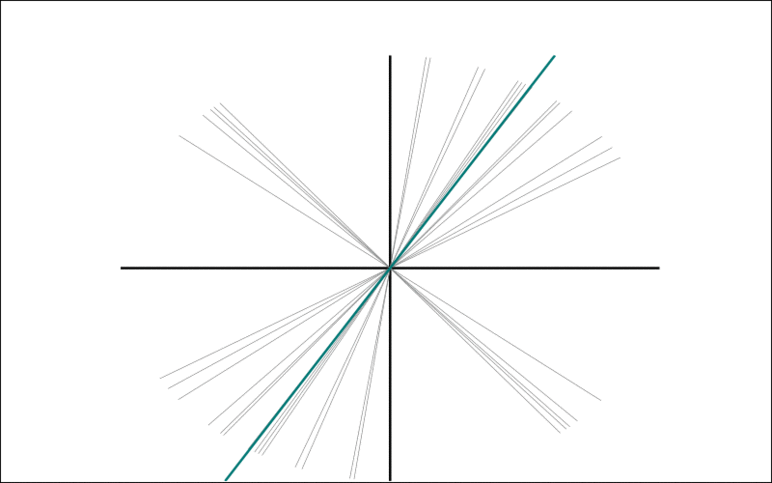
There are several ways to approach robust principal component analysis (RPCA). In early work [] we noted that PCA constructs a linear subspace that minimizes least squares reconstruction error of the data. Since least squares is not robust to ourliers, neither is standard PCA. We reformulated the reconstruction term robustly and solved for the subspace that minimized a robust error term. The approach worked well but was computationally expensive.
As the collection of large datasets becomes increasingly automated, the occurrence of outliers will increase -- big data implies big outliers. As a scalable approach to robust PCA we propose to compute the average subspace spanned by the data; this can then be made robust by computing robust averages [].
We note that in a zero-mean dataset, each observation spans a one-dimensional subspace, giving a point on the Grassmann manifold. We show that the average subspace corresponds to the leading principal component for Gaussian data. We provide a simple algorithm for computing this Grassmann Average (GA), and show that the subspace estimate is less sensitive to outliers than PCA for general distributions. Because averages can be efficiently computed, we immediately gain scalability. We exploit robust averaging to formulate the Robust Grassmann Average (RGA) as a form of robust PCA. The resulting Trimmed Grassmann Average (TGA) is appropriate for computer vision because it is robust to pixel outliers. The algorithm has linear computational complexity and minimal memory requirements. We demonstrate TGA for background modeling, video restoration, and shadow removal. We show scalability by performing robust PCA on the entire Star Wars IV movie; a task beyond any current method.
This page provides source code and video material for the paper Grassmann Averages for Scalable Robust PCA.
Members
Publications


