Adaptive Locomotion of Soft Microrobots
Networked Control and Communication
Controller Learning using Bayesian Optimization
Event-based Wireless Control of Cyber-physical Systems
Model-based Reinforcement Learning for PID Control
Learning Probabilistic Dynamics Models
Gaussian Filtering as Variational Inference
Electromechanics of planar HASEL actuators
Sophie Kirkman, Philipp Rothemund, Christoph Keplinger et. al., Extreme Mechanics Letters, 2021 []
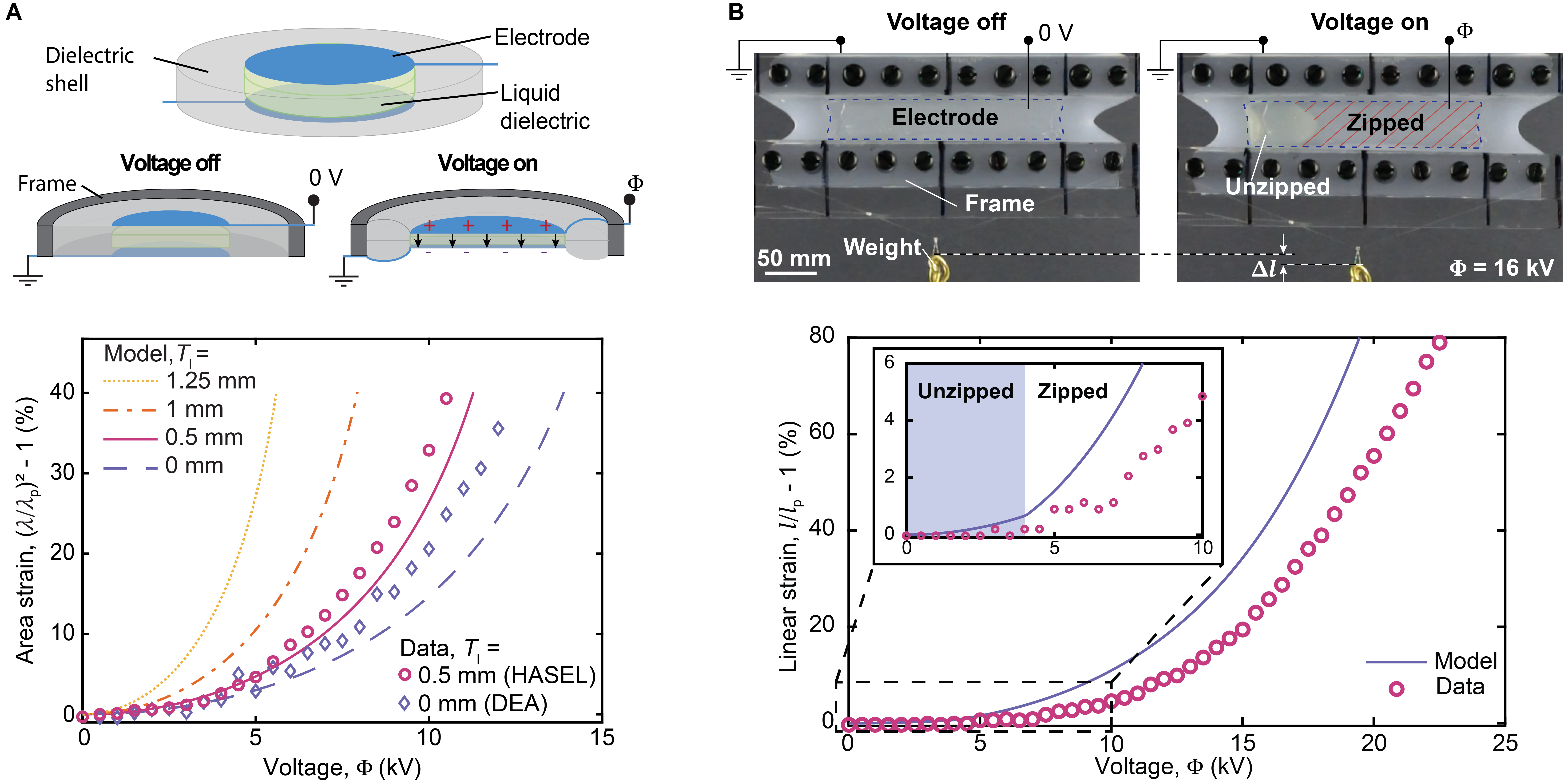
Planar HASEL (hydraulically amplified self-healing electrostatic) actuators are stretchable, soft artificial muscles, with self-healing properties and muscle-like performance []. They have, with 70 J/kg, greater specific energies than natural muscle, and have achieved specific powers of 614 W/kg and linear strains of 124%. While planar HASEL actuators had demonstrated strong performance in experiments, the details of the underlying electromechanics had not yet been explored.
Planar HASEL actuators comprise a stretchable dielectric shell that is coated with compliant electrodes and filled with a liquid dielectric. Upon electrical activation, they expand in-plane. In experiments, two mechanisms of deformation are observed: elastic stretching of the shell and electrohydraulic “zipping”, where the electrodes progressively come together. This project [] analyzed these mechanisms using two examples: a circular planar HASEL actuator that stretches equibiaxially, and a linear actuator that both stretches and zips.
To understand the quasistatic actuation behavior of planar HASELs, we used an energy minimization approach to derive a nonlinear electromechanical model for each geometry. For the circular HASEL actuator, we did a parametric study to elucidate the effect of the liquid layer. This analysis shows that the actuation behavior is similar to that of dielectric elastomer actuators (DEAs), and reveals how the added liquid layer in planar HASELs reduces their stiffness, allowing them to achieve greater strains than DEAs of the same dimensions. For the linear actuator, the model displays how the actuator only stretches until it reaches a critical voltage at which it starts to zip, drastically increasing strain.
The derived models show good quantitative agreement with measured data. This work lays the foundation for the theoretical analysis of planar HASEL actuators, which consist of stretchable materials.
Members
Publications


